Analysis of the Fill Ratio for gTLD Domain Zones

Most Internet users and even web-developers have no clue about the problem of getting the list of currently registered domains. Usually, we are greeting our customers when they are looking for domain lists to feed their crawlers, which are used for scraping some particular info from thousands of websites. At this point, they realize that there are a bunch of Registries restrictions on downloading such lists, and usually, they are not available to the public.

At one of our side projects, we are faced with the same kind of problem when started to develop our backlinks analyzing tool, which is preferable needed to go over all websites in the world and collect all links from them. So, we developed specialized crawlers which are started to work and follow the links to the web pages all over the Internet. And by following them, we were slowly getting our database of domain names. To make it current, we verified the domains via NS records and whois info, which was tricky as well.

Anyway, today we are going to focus on some analytical data we could get from out gTLD lists. First of all, let’s find out the fill ratio for different gTLD zones. To do so, we will start by finding out the total number of possible symbols/characters combinations. In ideal conditions according to Punycode you have 26 letters, 10 numbers and a tiny dash (‘-‘). So, for any TLD (top-level domain) or sub-domain, you have 37 names with only one symbol. Thus, sadly it’s not so easy to get such names. And 1369 names with two symbols, for instance, American Airlines are lucky guys who got aa.com. 50653 for three symbols, 1874161 for four, 69343…… bla bla bla 37^n for every next iteration. Here is you realize that even with five symbols you have an unimaginable amount of random combinations:

Number of symbols 1 , combinations : 37
Number of symbols 2 , combinations : 1369
Number of symbols 3 , combinations : 50653
Number of symbols 4 , combinations : 1874161
Number of symbols 5 , combinations : 69343957
Number of symbols 6 , combinations : 2565726409
Number of symbols 7 , combinations : 94931877133
Number of symbols 8 , combinations : 3512479453921
Number of symbols 9 , combinations : 129961739795077
Number of symbols 10 , combinations : 4808584372417849
Number of symbols 11 , combinations : 177917621779460413
Number of symbols 12 , combinations : 6582952005840035281
Number of symbols 13 , combinations : 243569224216081305397
Number of symbols 14 , combinations : 9012061295995008299689

To make it simpler to get, let’s think about this like buckets. We have 14 different buckets with a volume, which is shown above. And we are going to check how filled that buckets for different gTLDs. By the code below we are going thru gTLD zones data-set, counting the amounts of domain names with different numbers of symbols in them (filling the buckets for each particular zone). Also, I’m dropping off all third level+ domain names (like something.com.org for ex) to keep our research in the borders of gTLD zones.

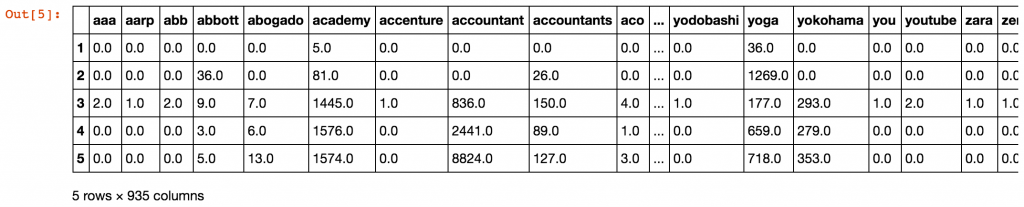
935

#let's check what we've got:
count_df.head()

And now, we’re ready to check the most frequent lengths for gTLD domain zones with more than 100K records:

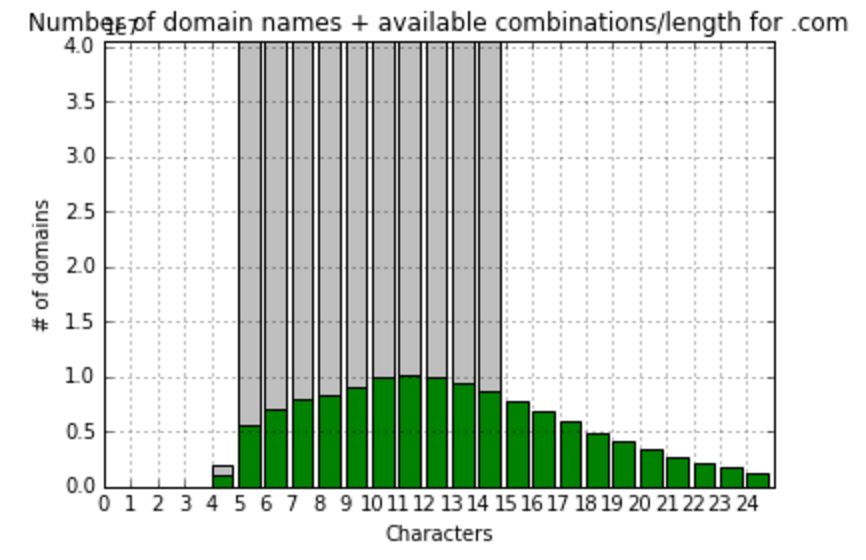
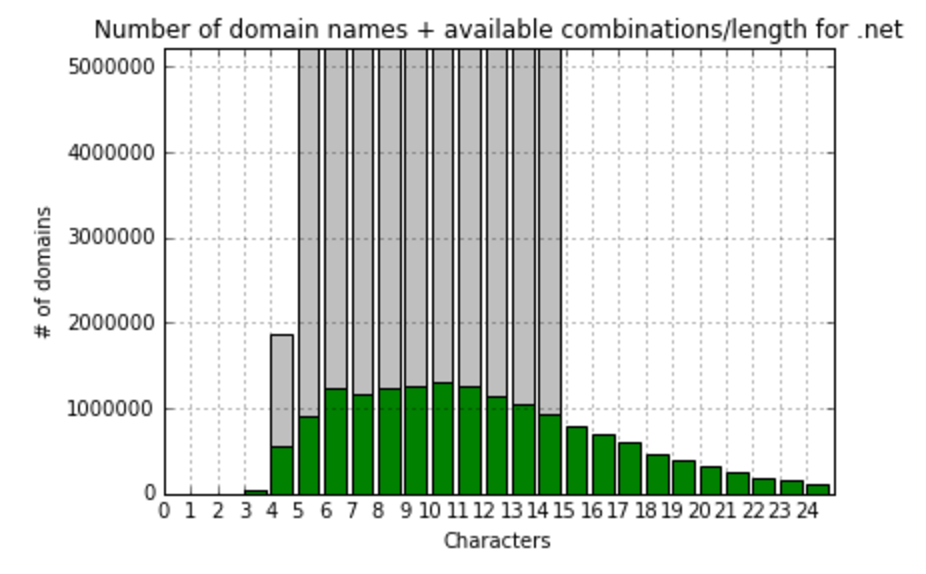
 .com most frequently (10145838 domains) domain name has 11 symbols in a name

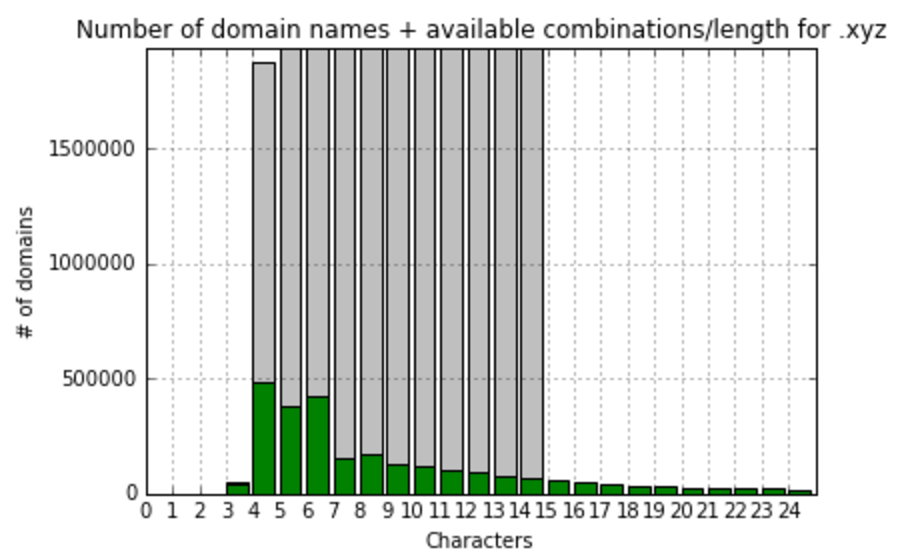
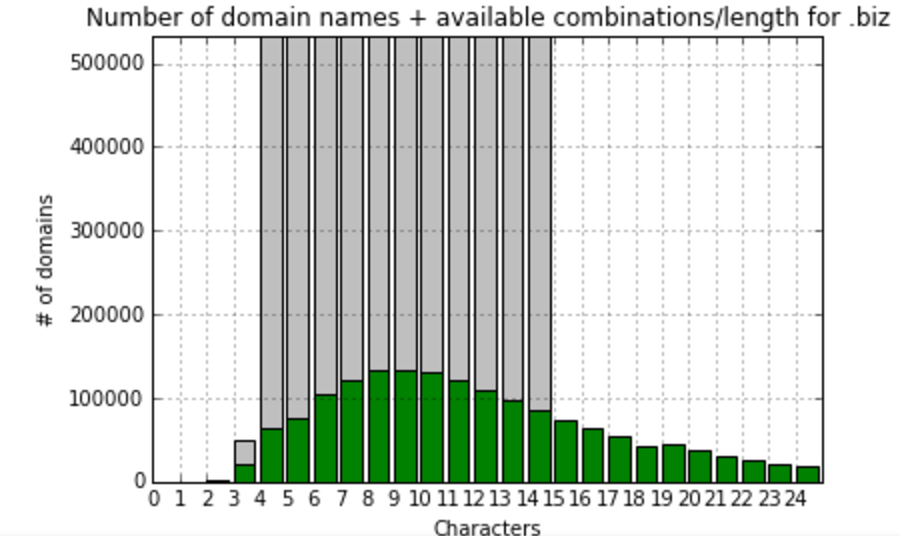
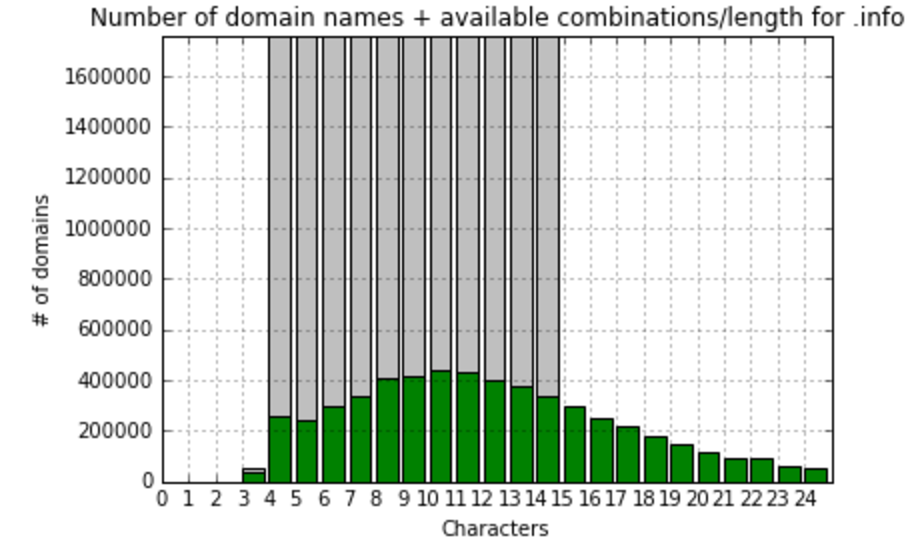
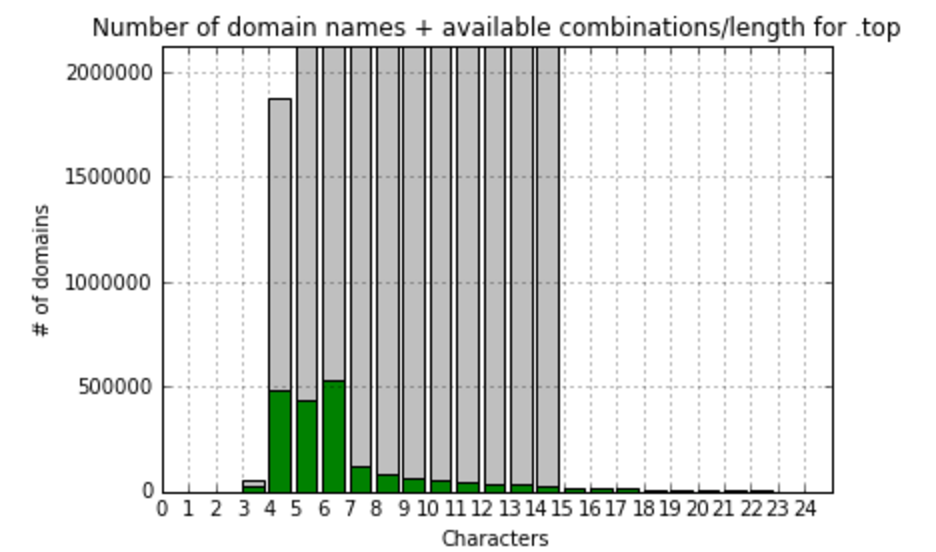
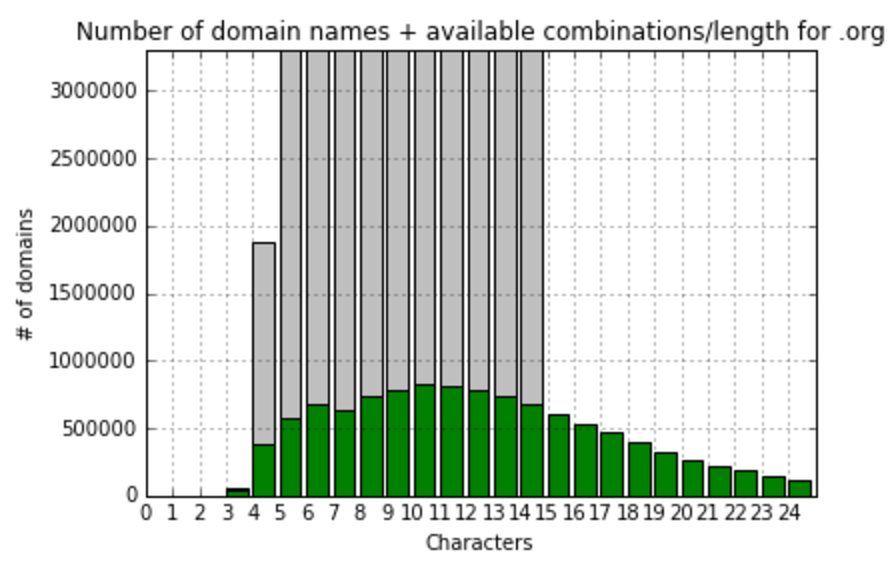
org:most frequently (826779 domains) domain name has 10 symbols in a name
top:most frequently (531985 domains) domain name has 6 symbols in a name
info:most frequently (440391 domains) domain name has 10 symbols in a name
net:most frequently (1307689 domains) domain name has 10 symbols in a name
com:most frequently (10145838 domains) domain name has 11 symbols in a name
biz:most frequently (133380 domains) domain name has 8 symbols in a name
xyz:most frequently (485177 domains) domain name has 4 symbols in a name

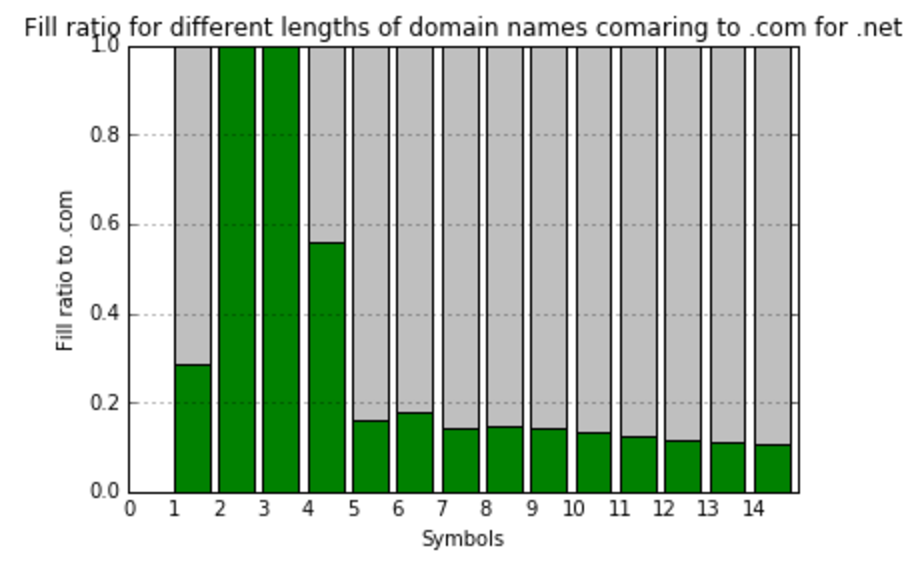
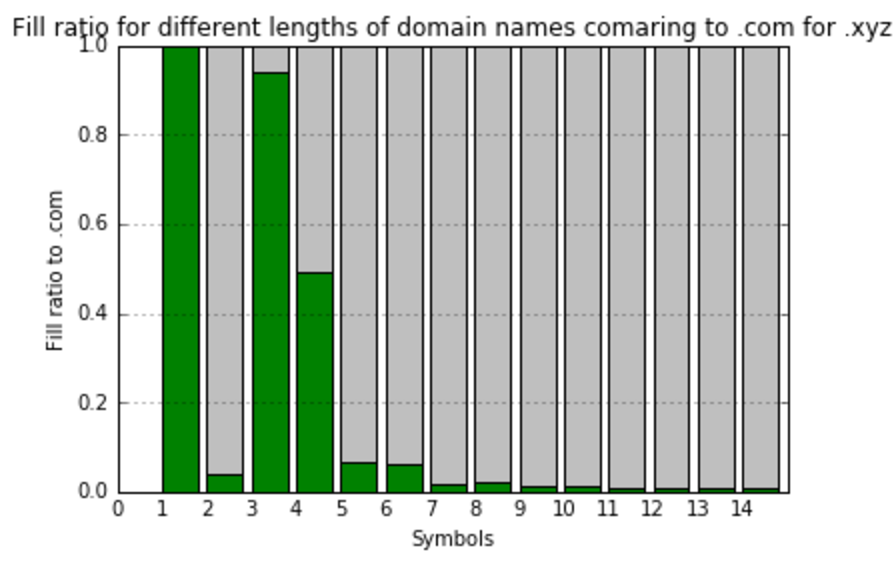
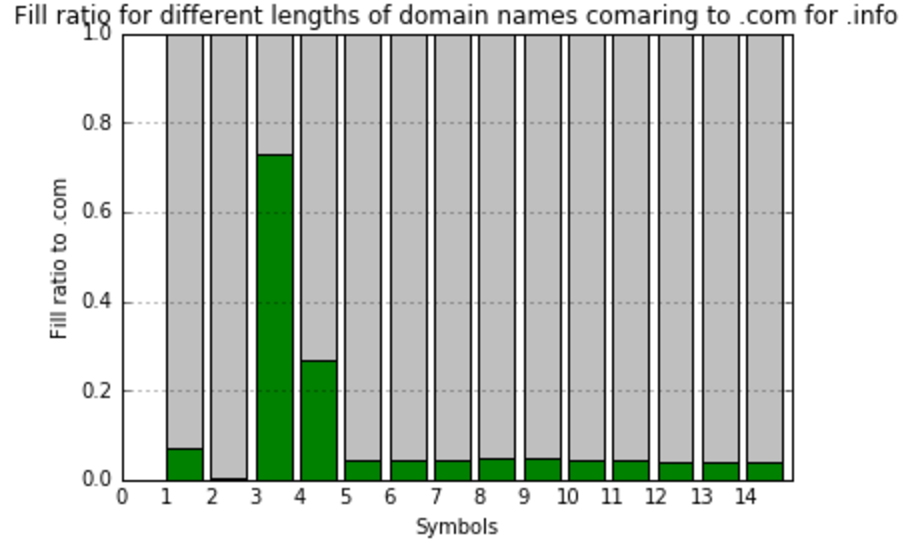
So, we see that in most popular zones names are usually consisted of 10-11 symbols, let’s focus on gTLD zones with more than 100K records and calculate fill ratio to maximum combinations and visualize it:

At this point, I’d realized that comparing to the total amount meaningless combinations do not show us anything useful. I’ve decided to create one more value – fill ratio to most filled gTLD zone – .com. So, here we’re calculating and visualizing that:

As you can see, the filling of different gTLDs has high variance. But, from the first look, it’s obvious that there is some clusters there, and TLDs can be classified by the way they filled. Thus, having those classifications in hands, we are ready to predict the future fill of TLDs.